Выпуск: №5(73) КОД науки – исследования молодых ученых

Раздел: Инновационные образовательные технологии

Опубликовано: 30 апреля 2025

Код уникальной десятичной классификации: 372.851

Автор: Смирнова Ирина Вадимовна

магистрант 2 курса, Московский городской педагогический университет (МГПУ), г. Москва, e-mail: smirnovaiv@mgpu.ru

Научный руководитель: Кочагина Мария Николаевна

заместитель начальника департамента по учебной работе, доцент департамента математики и физики Института цифрового образования Московского городского педагогического университета (МГПУ)

кандидат педагогических наук, доцент

Второе место конкурса «КОД науки» в номинации
«Инновационные образовательные технологии» (2025 г.)

Аннотация. В статье описывается применение опорных геометрических конструкций в обучении геометрии учащихся классов, обучающихся в рамках московских проектов «Математическая вертикаль» и «Московские математические классы». Автор предлагает использовать геометрические конструкции как эффективное средство обучения решению геометрических задач и демонстрирует способы включения геометрических конструкций в систему обучения геометрии.

Ключевые слова: обучение геометрии, обучение решению задач, геометрические конструкции, ключевые задачи, углубленный уровень.

В условиях современного мегаполиса, где информационные потоки становятся всё более интенсивными, а требования к квалификации специалистов всё выше, роль математического образования возрастает многократно. Математика не только формирует фундамент для развития естественных и технических наук, но и способствует развитию критического мышления, способности к анализу и синтезу информации, что является необходимым условием для успешной адаптации в быстроменяющемся мире. Выявление и развитие математических способностей у школьников является ключом к формированию кадрового потенциала для научных и технологических сфер.

В связи с этим 19 ноября 2024 года распоряжением Правительства Российской Федерации №3333-р был принят комплексный план мероприятий по повышению качества математического и естественно-научного образования до 2030 года [8].

Сегодня в системе московского образования функционирует более 60 специализированных школ и образовательных комплексов, реализующих программы углублённого обучения математике. Эти школы предлагают разнообразные программы, обеспечивающие углублённое изучение предмета с первых классов и до выпускного класса старшей школы. Они также активно взаимодействуют с ведущими вузами и научными организациями столицы, предоставляя учащимся возможности для углубления знаний и развития исследовательских навыков, например, СУНЦ МГУ, ГБОУ «Курчатовская школа» г. Москвы, ГБОУ «Лицей «Вторая школа» им. В.Ф. Овчинникова» г. Москвы, ГБОУ «Пятьдесят седьмая школа» г. Москвы, ГБОУ «Школа № 1568 имени Пабло Неруды» г. Москвы и другие.

Система московского образования предлагает различные формы углублённого изучения математики. В настоящее время московским школьникам предлагается изучать математику на углубленном уровне в рамках двух проектов «Математическая вертикаль» и «Московские математические классы».

Классы проекта «Математическая вертикаль»

Программа для учеников 7-9 классов, которая готовит их к обучению в предпрофессиональных классах. Проект «Математическая вертикаль» направлен на повышение качества математического образования и выявление талантливых школьников, на развитие их творческого потенциала в области математики. Этому способствуют отбор мотивированных учеников, увеличенное количество часов, кружки. Для проекта также созданы специальные учебные пособия. Обучение в таких классах помогает школьникам не только улучшить свои математические умения, но и подготовиться к поступлению в вузы на специальности, связанные с точными науками.

Проект «Московские математические классы»

Это проект, направленный на углублённое изучение математики в школах Москвы, показывающих высокие результаты математической подготовки школьников и имеющих богатые и давние традиции математического образования высокого уровня. Это достигается за счет увеличения количества часов математики в учебной программе, отбора мотивированных учащихся благодаря внутренним экзаменам для поступления. Его особенность заключается в создании специализированных классов, где обучение ведётся по программам высокого уровня и ориентировано на развитие математических способностей у учащихся.

Каждый проект имеет свои особенности и целевую аудиторию, что позволяет им эффективно дополнять друг друга в рамках системы математического образования в Москве. Система обучения математике в этих проектах строится на основе индивидуальных потребностей и интересов учащихся и включает в себя разнообразные формы работы, такие как лекции, семинары, практические занятия, а также участие в олимпиадах и конкурсах. Особое внимание уделяется развитию логического мышления, способности к абстрактному рассуждению и решению задач повышенной и высокой сложности.

Умение решать задачи включает умение проводить поиск решения задачи. На протяжении многих лет остаётся актуальной проблема обучения поиску решения планиметрических задач [12]. Различные авторы акцентируют внимание на важности использования наглядных пособий и моделей для развития пространственного мышления, предлагают активно применять чертежи, модели геометрических фигур и динамические иллюстрации, чтобы помочь ученикам лучше понять смысл геометрических теорем, подчёркивают необходимость систематической работы над развитием логического мышления и умения формулировать доказательства. Маршал Гордон указывает, что кроме обучения отдельным методам решения геометрических задач важно обучать эвристическим приемам, помогающим находить путь к решению задачи [15, с. 393].

Р.Г. Хазанкин и В.Ф. Шаталов [13] также предлагали свои методы для улучшения понимания геометрии. Р.Г. Хазанкин [14] акцентирует внимание на решении ключевых задач, которые помогают ученикам лучше понять основные принципы геометрии. В.Ф. Шаталов разрабатывал системы опорных сигналов и конспектов, которые упрощают восприятие, запоминание геометрических теорем и их применение при решении задач. Проблема в обучении геометрии часто заключается в том, что ученики не всегда могут визуализировать, представить себе геометрические конфигурации и увидеть необходимость использования той или иной теоремы. Для понимания требуется развитие пространственного воображения, и использование разнообразных методов и подходов может помочь ученикам лучше воспринимать и анализировать геометрические формы и их свойства.

Одним из путей решения данной проблемы может являться использование геометрических конструкций в обучении геометрии.

Геометрические конструкции представляют собой базовые модели и схемы, которые помогают учащимся лучше понять и усвоить геометрические конфигурации, соответствующие некоторому геометрическому утверждению, а также научиться применять их на практике. Е.В. Звежинская понимает под геометрической конструкцией «конструкции, свойства которых известны и позволяют открывать свойства геометрических фигур и связи между ними» [6, с. 105].

Вопросом использования геометрических конструкций в обучении геометрии занимались такие ученые, как Л.Л. Тухолко [5], Е.В. Звежинская [5], [6], Д. Пойа [12], В.В. Орлов [11] и другие. В своих исследованиях они разрабатывали различные способы применения геометрических конструкций.

Рассмотрим геометрические конструкции, представленные на рисунке 1. На чертежах (к одной и той же задаче) фигуры представлены так, что можно выделить геометрические конструкции, соответствующие некоторой теореме:

• на первом чертеже можно выделить два подобных треугольника;
• на втором чертеже отрезок , соединяющий основание двух высот остроугольного треугольника, отсекает от треугольника подобный ему треугольник;
• на третьем чертеже можно заметить выполнение условия существования описанной около четырехугольника окружности, а именно, если диагонали четырехугольника образуют прямые углы со сторонами, то он является вписанным в окружность.

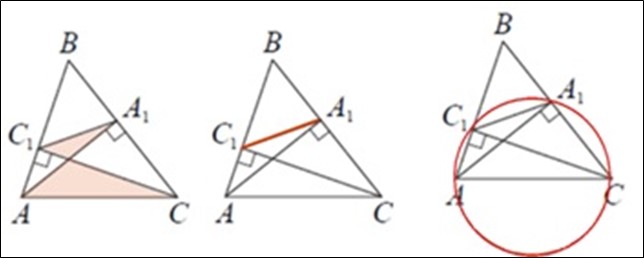
Рис. 1. Примеры геометрических конструкций

Между заданными на чертеже объектами можно уставить геометрический факт, который выражается в некотором геометрическом утверждении (свойстве или признаке некоторого объекта). Установление этого факта вскрывает неявные связи между объектами, заданными в задаче, что может привести к решению задачи. Следовательно, применение геометрических конструкций при решении задач выполняет эвристические функции.

В рамках исследования было произведено описание геометрических конструкций, обладающих дидактическим потенциалом для формирования умений решать задачи по геометрии.

Геометрическая конфигурация 1. Медиана прямоугольного треугольника, проведённая к гипотенузе, равна её половине. (см. рисунок 2).

На рисунке 2 изображён прямоугольный треугольник ABC (∠C = 90°), в котором проведена медиана СМ, тогда можно сделать вывод о том, что .

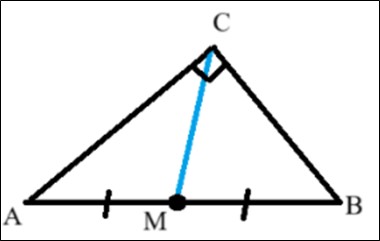
Рис. 2. Чертеж геометрической конфигурации 1

Геометрическая конфигурация 2. Признаком прямоугольного треугольника является равенство медианы треугольника половине стороны, к которой она проведена

(см. рисунок 3).

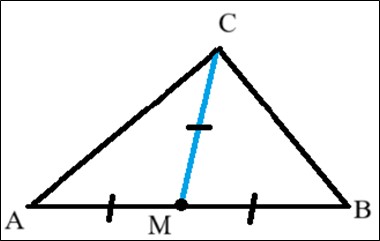
Рис. 3. Чертеж геометрической конфигурации 2

Эти две конструкции иллюстрируют свойство и признак прямоугольного треугольника. Эвристика в решении задач при наличии элементов конструкции – медиана треугольника, равная половине стороны, к которой она проведена, указывает на прямоугольный треугольник. Если в задаче присутствуют не все элементы конструкции, то дополняя ее другими элементами конструкции, можно получить дополнительную информацию, которая возможно поможет решить задачу.

Задачи, которым соответствуют конфигурации 1-2, можно предложить учащимся в качестве ключевых задач [10, с. 129].

Использование геометрических конструкций в качестве базовых моделей способствует не только усвоению учащимися алгоритмов решения, но и развитию геометрической интуиции посредством запоминания и припоминания характерных конструкций.

Кроме выделения геометрических конструкций, их усвоения и формирования умения видеть их на чертеже, на следующих этапах обучения необходимо организовать самостоятельное решение задач обучающимися на основе усвоенных геометрических конструкций. В качестве иллюстрации можно привести примеры задач на применение изучаемых геометрических конструкций и охарактеризовать рассуждения на разных этапах ее решения. Также можно предложить обучающимся сформулировать собственные задачи, используя в качестве основы рассмотренные геометрические конструкции.

Задача 1
Любой треугольник можно разрезать на равнобедренные треугольники.

Анализ задачи. Дан произвольный треугольник. Задача сводится к построению отрезков, по которым нужно произвести разрезания, чтобы получить равнобедренные треугольники – треугольники с равными сторонами. Если сможем указать такой способ построения, то задача будет решена.

Поиск решения и построение модели. Анализируя способ получения равнобедренного треугольника, приходим к необходимости использования определения или признака равнобедренного треугольника. Наличие двух равных сторон приводит к необходимости введения их на чертеже, что напоминает геометрическую конструкцию 2, но только в случае прямоугольного треугольника (см. рисунок 3). Он на чертеже отсутствует, но его всегда можно получить, используя дополнительное построение – высоту треугольника. (см. рисунок 4). Геометрическая конфигурация подсказала введение в рассмотрение прямоугольного треугольника.

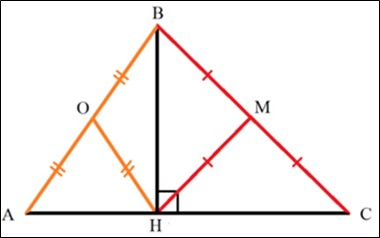
Рис. 4. Чертеж задачи 1

1. В треугольнике можно провести хотя бы одну высоту, находящуюся внутри ΔBCH: BH ⊥ AC.
2. По свойству прямоугольного треугольника ΔBCH: проведем HM – медиану => BM = MH = =HC.
3. Аналогично для ΔABH: HO = BO = AO.
4. Получили 4 равнобедренных треугольника.
   Что и требовалось доказать.

Познавательный анализ. Геометрическая конструкция 2 позволила увидеть необходимость дополнительного построения в задаче.

Задача 2
В остроугольном треугольнике АВС высоты AE и BF пересекаются в точке Н, точки M и N середины стороны АВ и НС соответственно. Докажите, что МН и FE перпендикулярны. (см. рисунок 5).

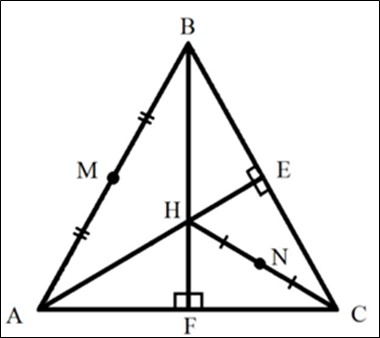
Рис. 5. Чертеж и краткое условие задачи 2

Дано:
Δ ABC – остроугольный,
AE – высота, BF – высота,
AE ∩BF = H, M – середина AB, N – середина HC,
Доказать: MH ⊥ FE.

Анализ задачи. В остроугольном треугольнике проведенные высоты разбивают его на прямоугольные треугольники. Середины сторон лежат на сторонах образовавшихся прямоугольных треугольников. Можно получить равнобедренные треугольники, в которых медиана будет также являться высотой. Если получится найти равнобедренные треугольники, у которых совпадает основания, а вершины лежат в разных полуплоскостях относительно основания – задача будет решена.

Поиск решения и построение модели. Геометрическая конфигурация 1 подсказывает введение в рассмотрение прямоугольных треугольников, а также проведение медиан, поскольку в треугольниках отмечены середины гипотенуз. Причем один и тот же отрезок включен в прямоугольные треугольники. Значит, получаем равные отрезки, являющиеся боковыми сторонами равнобедренных треугольников с общим основанием. (см рисунок 6). Замечаем, что отрезки равнобедренного треугольника находятся на одинаковом расстоянии от основания, что является признаком серединного перпендикуляра.

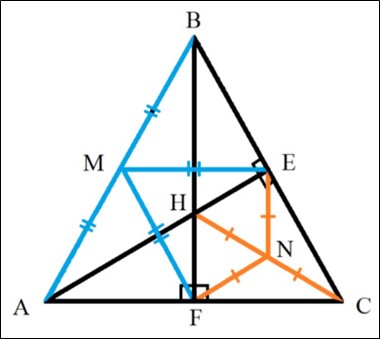
Рис. 6. Чертеж задачи 2

1. MF – медиана Δ AFB, EM – медиана Δ AEB.
2. Значит, MF=ME.
3. FN – медиана Δ FHC, NE – медиана Δ HEC.
4. Значит, EN = NF.
5. из пунктов 1-2 следует, что FE⊥ MN (по признаку серединного перпендикуляра).
   Что и требовалось доказать.

Познавательный анализ. Геометрическая конструкция 1 позволила увидеть необходимость дополнительного построения в задаче.

Конфигурация «медиана равна половине стороны, к которой проведена» является ключевым элементом в решении ряда геометрических задач. Она позволяет выявить прямоугольные треугольники, а также использовать их свойства для доказательства или нахождения неизвестных величин. Умение распознавать и достраивать эту конфигурацию помогает учащимся установить неявные связи в задаче, понять ее структуру и выбрать правильный путь к её решению.

Использование геометрических конструкций на уроке математики может быть эффективным на разных его этапах. На этапах актуализация знаний или первичного закрепления материала геометрические конструкции могут быть полезны в задачах на готовых чертежах [4, с 10]. Это помогает учащимся увидеть конструкции на предложенном готовом чертеже без необходимости строить чертеж к задаче.

При введении новой геометрической конструкции эффективным подходом может быть рассмотрение ключевой задачи [14]. В этом случае важно на этапе познавательного анализа задачи уделить особое внимание геометрической конструкции на чертеже, которая помогает решить задачу. Такой метод способствует более глубокому пониманию материала и развитию навыков аналитического мышления у учащихся.

Геометрические конструкции можно использовать в обучении учащихся как на углубленном, так и на базовом уровне. Однако, их использование приобретает особую значимость при работе с учащимися, изучающими математику на углубленном уровне, поскольку здесь они являются необходимым инструментом для эффективного поиска решений нестандартных задач.

Геометрические конструкции при обучении учащихся классов проектов «Математическая вертикаль» и «Московские математические классы» могут быть использованы для обучения приемам поиска решения геометрических задач; систематизации знаний, визуализации геометрических конфигураций, развития пространственного воображения обучающихся. Такая работа уже ведется с учащимися, изучающими математику на углубленном уровне в ГБОУ «Школа №1568 имени Пабло Неруды» г. Москвы.

Таким образом, использование геометрических конструкций представляется важным инструментом для обучения решению геометрических задач в основной школе.

В заключение хотелось бы привести слова Д. Пойя «Чтобы научить решать задачи, надо их решать» [12, с. 13], и добавить: «С использованием геометрических конструкций!»

Список литературы:

1. Волхонская А.С, Кочагина М.Н. Обучение школьников решению геометрических задач с помощью свойств центра масс // Казанская наука, 2024. №5. С. 40-44.
2. Гнеденко Б.В. Из истории математики и ее преподавания в России // Математика в школе, 2012. №7. С. 61-67.
3. Денищева Л.О. Теория и методика обучения математике в школе. Учебное пособие / Л.О. Денищева, А.Е. Захарова, М.Н. Кочагина [и др]. М.: БИНОМ. Лаборатория знаний, 2011. 413 с.
4. Задачи по геометрии. Дополняем школьный учебник: методическое пособие / М.Н. Кочагина, С.М. Даниелян, В.В. Кочагин [и др.]. М.: МГПУ, 2024. 124 с.
5. Звежинская Е.В. Методика формирования умения распознавать ключевые геометрические конструкции при решении задач // Студенческая наука – инновационный потенциал будущего: сб. ст. междунар. форума. студен. науки / редкол. А.В. Торхова [и др.]. Минск: 2022. С. 60-63.
6. Звежинская Е.В., Тухолко Л.Л. Эвристическая функция геометрических конструкций в курсе планиметрии // Материалы Международная студенческая научно-практическая интернет-конференция «Инновационные подходы к обучению физике, математике, информатике», Минск: БГПУ, 2021. С. 104-107.
7. Козлова Н.И., Иванова А.М., Путушкина М.Г. Методические особенности организации и проведения урока одной задачи // Лига исследователей МГПУ: сборник статей. Москва, 20-24 ноября 2023 года. М.: ПАРАДИГМА, 2023. С. 85-92.
8. Концепция развития математического образования в Российской Федерации: (утв. распоряжением Правительства РФ от 19 ноября 2024 г. № 3333-р). (дата обращения 03.04.2025).
9. Кочагина М.Н., Шикунова А.П. «Семьи» понятий и их использование в обучении решению геометрических задач в 7-9 классах // Сборник трудов VII Международной научно-методической конференции «Эвристическое обучение математике». Донецк: Донецкий национальный университет, 2024. С. 37-42.
10. Мерзляк А.Г., Поляков В.М. Геометрия: 7 класс: учебник: углубленный уровень / под ред. В.Е. Подольского. М.: Просвещение, 2024. 208 с.
11. Орлов В.В. Геометрия в задачах, 7-8 классы: пособие для ученика и учителя. СПб.: Интерлайн, 1999. 212 с.
12. Пойя Д. Как решать задачу. М.: Либроком, 2010. 208 с.
13. Шаталов В.Ф., Шейман В.М., Хаит А.М. Опорные конспекты по кинематике и динамике. Из опыта работы. Книга для учителя. М.: Просвещение, 1989. 142 с.
14. Фоминых Ю.Ф., Плотникова Е.Г. Педагогика математики. Пермь: 2000. 460 с.
15. Marshall Gordon. Teaching Mathematics: Heuristics Can and Ought to Lead the Way, Journal of Humanistic Mathematics, Volume 11 Issue 2 (July 2021).: 392-404.

Geometric patterns like tools for teaching geometry to students at an advanced level

Smirnova I.V.,
undergraduate of 2 course of the Moscow City University, Moscow

Research supervisor:
Kochagina Maria Nikolaevna,
Deputy Head of the Department for Academic Affairs, Associate Professor of the Department of Mathematics and Physics of the Institute of Digital Education of Moscow City University, Candidate of Pedagogical Sciences, Associate Professor

Abstract. The article describes the use of supporting geometric constructions in teaching geometry to students of classes studying within the framework of the Moscow projects «Mathematical Vertical» and «Moscow Mathematical Classes». The author proposes to use geometric constructions as an effective means of teaching geometric problem solving and demonstrates the ways of including geometric constructions in the system of teaching geometry.
Keywords: geometry teaching, teaching problem solving, geometric constructions, key tasks, advanced level.

References:

1. Volkhonskaya A.S., Kochagina M.N. Teaching schoolchildren to solve geometric problems using the properties of the center of mass // Kazan Science, 2024. №5.: 40-44.
2. Gnedenko B.V. From the history of mathematics and its teaching in Russia // Mathematics at school, 2012. №7. 61-67.
3. Denishcheva L.O. Theory and methodology of teaching mathematics at school. Textbook / L.O. Denishcheva, A.E. Zakharova, M.N. Kochagina [et al.]. Moscow: BINOM. Laboratory of Knowledge, 2011. 413 p.
4. Geometry problems. We supplement the school textbook: a methodological guide / M.N. Kochagina, S.M. Danielyan, V.V. Kochagin [et al.]. Moscow: Moscow City University, 2024. 124 p.
5. Zvezhinskaya E.V. Methodology for the formation of the ability to recognize key geometric structures when solving problems // Student science – the innovative potential of the future: collection of international articles. the forum. Student of Science / editor. A.V. Torkhova [et al.]. Minsk: 2022.: 60-63.
6. Zvezhinskaya E.V., Tukholko L.L. Heuristic function of geometric constructions in the course of planimetry // Materials of the International Student Scientific and Practical Internet Conference «Innovative approaches to teaching physics, mathematics, and computer Science». Minsk: BSPU, 2021.: 104-107.
7. Kozlova N.I., Ivanova A.M., Putushkina M.G. Methodological features of organizing and conducting a lesson of one task // League of Researchers of the Moscow State Pedagogical University: collection of articles. Moscow, November 20-24, 2023. Moscow: PARADIGMA, 2023.: 85-92.
8. The concept of the development of mathematical education in the Russian Federation: (approved by Decree of the Government of the Russian Federation dated November 19, 2024, №3333-r). (date of the address: 03.04.2025).
9. Kochagina M.N., Shikunova A.P. «Families» of concepts and their use in teaching geometric problem solving in grades 7-9 // Proceedings of the VII International Scientific and Methodological Conference «Heuristic teaching Mathematics». Donetsk: Donetsk National University, 2024.: 37-42.
10. Merzlyak A.G., Polyakov V.M. Geometry: 7th grade: textbook: advanced level / edited by V.E. Podolsky. Moscow: Prosveshchenie, 2024. 208 p.
11. Orlov V.V. Geometry in problems, grades 7-8: handbook for students and teachers. St. Petersburg: Interline, 1999. 212 p.
12. Poya D. How to solve a problem. Moscow: Librocom, 2010. 208 p.
13. Shatalov V.F., Sheiman V.M., Chait A.M. Basic notes on kinematics and dynamics. From work experience. A book for teachers. Moscow: Prosveshchenie, 1989. 142 p.
14. Fominykh Yu.F., Plotnikova E.G. Pedagogy of mathematics. Perm: 460 p.
15. Marshall Gordon. Teaching Mathematics: Heuristics Can and should Guide, Journal of Humanistic Mathematics, Volume 11, Issue 2 (July 2021).: 392-404.