Аннотация. В данной статье проведено глубокое исследование методов вычисления египтянами объёмов пирамид. Автор статьи, на основе задачи №14 Московского математического папируса Голенищева, попыталась восстановить их метод вычисления объёма пирамиды без интегрального исчисления.
Египетские пирамиды признаны одним из семи чудес света. И при этом, это единственное из всех чудес, дошедшее до наших дней.
Но пирамиды – это не просто гигантский артефакт, это памятник египетским математикам. Такой же памятник, как Московский математический папирус Голенищева и Математический папирус Ринда. Пирамиды являются практическим дополнением к теоретическим расчётам, изложенным древнеегипетскими геометрами на папирусах. Математические достижения египтян даже для современного человека не утратили своего значения. Например, их метод вычисления объёма пирамиды без использования интегрального исчисления.
В данной статье мы попытаемся восстановить весь ход рассуждений египетских математиков, результатом которого будет доказательство формул для вычисления объёмов не только любой пирамиды, но и усечённой пирамиды.
Геометрия египтян начиналась с изучения простейшей фигуры – куба. Вычисление его объёма несложно. Объём куба равен произведению трёх его взаимно перпендикулярных рёбер: V=a×a×a, а число его граней равно 6.
На игральных костях, самые древние из которых найдены в Египте, видна нумерация граней куба, выполненная в классической египетской традиции записи цифр (см. рисунок 1).
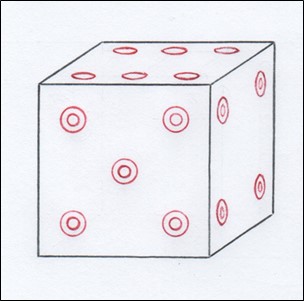
Рис. 1. Игральная кость, изобретённая в Древнем Египте
Теперь разрежем куб, как показано на рисунке 2.
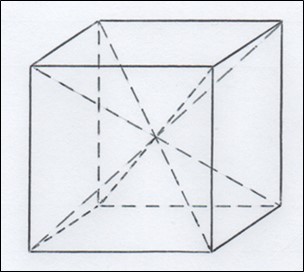
Рис. 2. Куб, разрезанный на 6 равных пирамидок
В результате куб распадается на 6 равных пирамидок. Объём каждой соответственно равен 1/6 объёма бывшего куба (см. рисунок 3).
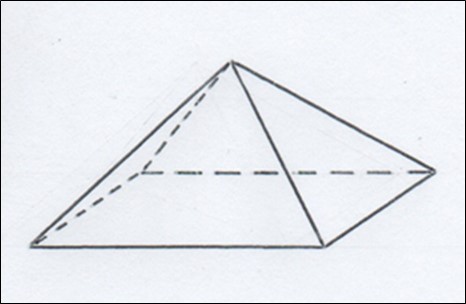
Рис. 3. Одна из шести пирамидок, вырезанных из куба
Учитывая, что в основании каждой из них лежит квадрат, площадь которого равна S=a², а высота h=1/2а, получаем первую формулу для простейшей пирамиды с квадратом в основании V=1/3×S×h. Естественно, мы рассмотрели частный случай.
Чтобы перейти к общему доказательству, обратим внимание на задачу №14 из Московского математического папируса Голенищева, перевод которой впервые был осуществлён великим русским египтологом Б.А. Тураевым, а опубликован на русском языке в статье Д.П. Цинзерлинга [1], [2]. Там шла речь о вычислении объёма усечённой пирамиды с квадратом в основании. Также был представлен чертёж, из которого следует, что усечённая пирамида была рассечена плоскостью, проходящей через середину её высоты параллельно плоскости основания пирамиды. Это очень важная деталь, содержащая в себе подсказку о том, как египтяне решали задачу о вычислении объёма пирамиды.
Прежде чем перейти к выводу формулы для вычисления объёма пирамиды, рассмотрим две простых леммы.
Лемма 1
Если мы имеем два подобных прямоугольных параллелепипеда, таких, что рёбра второго отличаются по величине от рёбер первого в k раз (см. рисунок 4), то объём второго прямоугольного параллелепипеда равен объёму первого, умноженному на k в кубе: V₂=V₁×k³.
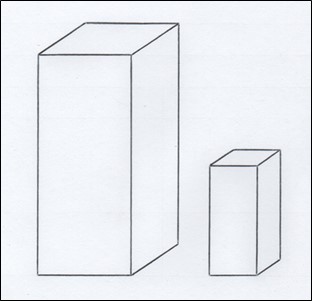
Рис. 4. Два подобных прямоугольных параллелепипеда
Лемма 2
Если в оба подобных прямоугольных параллелепипеда (см. лемму 1) вписаны пирамиды (см. рисунок 5), то объём второй вписанной пирамиды равен объёму первой вписанной пирамиды, умноженному на k в кубе.
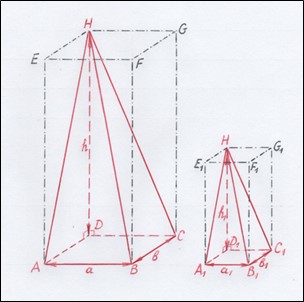
Рис. 5. Пирамиды, вписанные в подобные прямоугольные параллелепипеды

Теперь переходим собственно к выводу и доказательству формулы объёма пирамиды на основе подсказки, существующей в задаче №14 папируса Голенищева. То есть, будем использовать такую же усечённую пирамиду, как рассмотренная в задаче №14, у которой сечение прошло параллельно основанию через середину высоты. Достроим эту усечённую пирамиду АВСDA₁B₁C₁D₁ до её первоначального вида, когда она не была рассечена (см. рисунок 6).

Рис. 6. Усечённая пирамида, достроенная до полной пирамиды
Получаем пирамиду ABCDH, особенностью которой является то, что её высота совпадает с одним из боковых рёбер.
Проведём два сечения этой пирамиды вертикальными плоскостями через отрезки A₁B₁ и B₁C₁, как показано на рисунке 7.
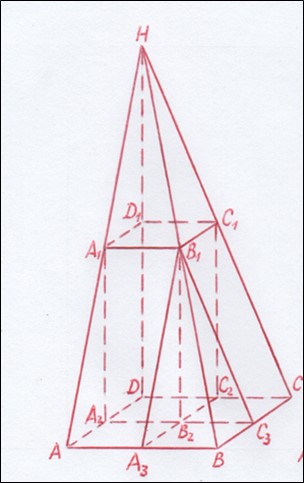
Рис. 7. Сечение пирамиды вертикальными плоскостями A₂A₁B₁C₃ и A₃B₁C₁C₂
Обозначим: AB=a, A₁B₁=1/2a, BC=b, B₁C₁=1/2b, DH=h, D₁H=B₂B₁=1/2h
Таким образом, пирамида получается разделённой на 5 частей (тремя плоскостями: 1 – плоскостью, проходящей через середину высоты параллельно плоскости основания пирамиды; 2 – плоскостью, проходящей через отрезок A₁B₁ перпендикулярно плоскости основания пирамиды; 3 – плоскостью, проходящей через отрезок B₁C₁, перпендикулярно плоскости основания пирамиды). Фигуры, полученные от такого деления пирамиды, для наглядности показаны на рисунке 8.

Рис. 8. Фигуры, полученные от деления пирамиды

В итоге, собрав объёмы прямоугольного параллелепипеда, двух половинок прямоугольных параллелепипедов и двух малых пирамид и приравняв их сумму к объёму большой пирамиды, мы получили формулу для вычисления объёма пирамиды, которой пользовались в своих расчётах египтяне: V=1/3×S×h, где S=a×b – это площадь основания пирамиды, а h – высота пирамиды.
Пирамиду с рисунка 7 можно четырёхкратно отмультиплицировать до симметричной классической пирамиды (см. рисунок 9).
 |
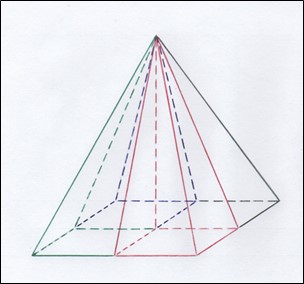 |
Рис. 9. Четырёхугольная пирамида с прямоугольником в основании
Четыре одинаковых пирамиды, имеющие высоту, которая совпадает с одним из боковых рёбер каждой, состыкованы по этой высоте (см. рисунок 9).
Для такой пирамиды также верна формула V=1/3×S×h.
Высота пирамиды может быть любой, а в основании может быть как прямоугольник, так и квадрат. Причём, основание высоты может не совпадать с центром прямоугольника в основании. И всё равно формула V=1/3×S×h будет справедлива, так как такая пирамида может быть разрезана на четыре элементарных пирамиды, у которых высота совпадает с одним из боковых рёбер (см. рисунок 10).
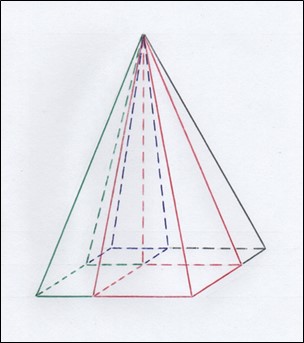
Рис. 10. Несимметричная прямоугольная пирамида
К сожалению, из-за ограниченности дошедших до нас математических артефактов Древнего Египта, у нас нет доказательств того, что египтяне вычисляли по этой же формуле объёмы наклонных пирамид. Впрочем то, что объём наклонной пирамиды будет равен одной трети произведения площади основания на высоту такой пирамиды, достаточно легко доказывается (см. рисунок 11).
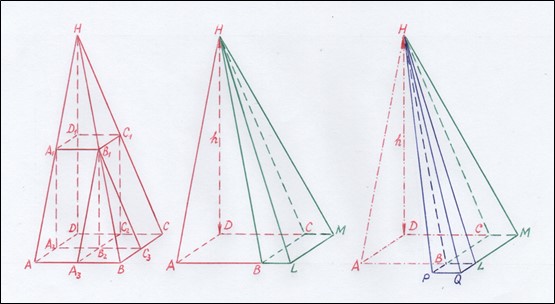
Рис. 11. Наглядная последовательность доказательства формулы V=1/3×S×h для наклонной пирамиды
На этом рисунке мы видим, что объём наклонной пирамиды BLMCH равен разности объёмов двух пирамид: ALMDH и ABCDH, у которых высота совпадает с боковым ребром. А затем мы видим, что объём наклонной пирамиды PQLBH равен разности объёмов двух других наклонных пирамид: PQMCH и BLMCH, у которых высота лежит в плоскости одной из боковых граней. А мы на примере пирамиды BLMCH уже доказали, что для таких пирамид верна та же формула: V=1/3×S×h.
Таким образом, и для наклонной прямоугольной пирамиды действует формула: V=1/3×S×h, где S – площадь прямоугольного основания пирамиды, а h – её высота.
В итоге, обходясь без интегрального исчисления, мы получили очень важную формулу для вычисления объёма любой прямоугольной пирамиды.
Делая основание пирамиды сколь угодно малым прямоугольником, мы можем заполнить такими малыми площадями сколь угодно точно площадь любой конфигурации, что даёт нам возможность пользоваться формулой V=1/3×S×h и для конуса, и для любой конусоподобной фигуры (см. рисунок 12).
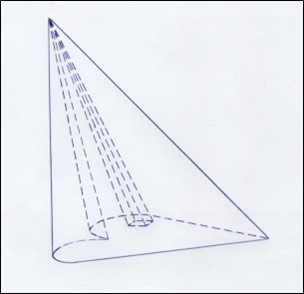
Рис. 12. Произвольная конусоподобная фигура с выделенным в ней малым элементом в виде пирамиды
Но эти математические рассуждения уже выходят за рамки нашей статьи, поэтому переходим к заключительной части наших расчётов, касающихся вычисления древними египтянами объёма усечённой пирамиды, подобной той, что описана в задаче №14 из Московского математического папируса Голенищева (см. рисунок 6).

Обычно эту формулу используют в комментариях к задаче №14 папируса Голенищева. Но если внимательно проследить за ходом решения этой задачи, записанным в Московском математическом папирусе, то мы видим, что египтяне использовали для вычисления объёма усечённой пирамиды формулу другого вида. А именно: V=1/3×∆h×(a²+a×a₁+a₁²), где – сторона квадрата нижнего основания усечённой пирамиды, – сторона квадрата верхнего основания усечённой пирамиды, а ∆h=h–h₁. Эту формулу можно получить, суммируя объёмы фигур, полученных при рассечении усечённой пирамиды вертикальными плоскостями (по типу сечения пирамиды на рисунке 7).

Но вернёмся к великим египетским артефактам. Легко заметить, что, достраивая пирамиду из задачи №14 папируса Голенищева до симметричной формы (см. рисунок 9), мы получаем форму пирамиды, типичную не для Северного Египта, а для Нубии (см. рисунок 13).
 |
 |
Рис. 13. Пирамиды Нубии
Необходимо отметить, что древние жители Северного Египта при строительстве пирамид с квадратом в основании, исходили из строгого правила, что высота пирамиды должна составлять 2/3 от стороны квадрата основания (см. рисунок 14).

Рис. 14. Пирамиды Северного Египта
Дробь 2/3 имела важное значение в египетском счислении. Для неё даже использовался специальный иероглиф (см. рисунок 15).
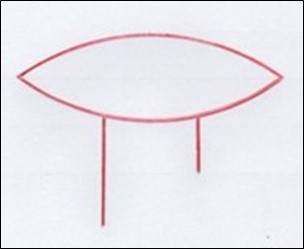
Рис. 15. Иероглиф, обозначающий дробь 2/3
Как известно, египтяне допускали запись иероглифов, как справа налево, так и слева направо. Для рисунка 15 выбран вариант из надписи, которую следует читать слева направо.
В большинстве геометрических задач о квадратных пирамидах, изложенных в папирусе Ринда [4], отношение высоты пирамиды к стороне квадратного основания равно 2/3.
Однако, в задаче №14 Московского математического папируса Голенищева отношение высоты к стороне квадратного основания составляет не 2/3, а 3/2. Можно предположить, что моделью для этой задачи послужили пирамиды Нубии, у которых отношение высоты к стороне квадратного основания составляло именно 3/2 (см. рисунок 16).
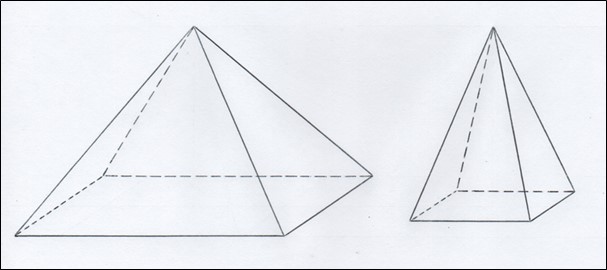
Рис. 16. Сравнение пирамиды Северного Египта (слева) с пирамидой Нубии (справа)
На то, что нубийские пирамиды могли послужить моделью для задачи №14 папируса Голенищева указывают данные замеров геометрических параметров нубийских пирамид, у которых угол наклона боковой грани к плоскости основания составляет ~70° [3]. А угол наклона грани к плоскости основания в задаче №14 Московского математического папируса Голенищева составляет ~71,5°, что с учётом погрешности, вызванной неидеальной сохранностью нубийских пирамид, является убедительным подтверждением нашей гипотезы.
Исходя из вышесказанного, можно допустить, что Математический папирус Ринда был написан египетским математиком из Северного Египта, а Московский математический папирус Голенищева был написан математиком, жившим в Южном Египте.
Список литературы:
- Костюк В.Я. О папирусе Голенищева и задачах №14 и №4 // «Наука в Мегаполисе. Science in a Megapolis», 2025. №12(80). (дата обращения: 06.11.2025).
- Цинзерлинг Д.П. Геометрия у древних египтян// Извѣстія Россiйской Академіи Наукъ. VI серiя, том 19, выпуск 12, 1925. С. 541-568. (дата обращения: 06.11.2025).
- Нубийские пирамиды. Википедия. (дата обращения: 10.11.2025).
- Arnold Buffum Chace. The Rhind Mathematical Papyrus / Arnold Buffum Chace, Ludlow Bull, Henry Parker Manning // Volume II, Mathematical Association of America, 1929. (дата обращения: 06.11.2025).
How the ancient Egyptians calculated the volume of a pyramid without integral calculus
Kostyuk V.Y.,
student of 3 course of the Moscow City University, Moscow
Abstract. In this article a deep study of the methods used by the Egyptians to calculate the volumes of the pyramids is conducted. The author of the article, based on problem №14 of the Golenishchev Mathematical Papyrus, tried to restore their method of calculating the volume of a pyramid without integral calculus.
Keywords: the Golenishchev Mathematical Papyrus, problem №14, Turaev B.A., integral-free calculation of the volume of a pyramid, the Nubian pyramids.
References:
- Kostyuk V.Y. About the Golenishchev Papyrus and Problems №14 and №4 // Science in a Megapolis, 2025. №12(80). (date of the address: 06.11.2025).
- Zinzerling D.P. Geometry of the ancient Egyptians // Proceedings of the Russian Academy of Sciences. VI Series, Volume 19, Edition 12, 1925.: 541-568. (date of the address: 06.11.2025).
- Nubian pyramids. Wikipedia. (date of the address: 10.11.2025).
- Arnold Buffum Chace. The Rhind Mathematical Papyrus / Arnold Buffum Chace, Ludlow Bull, Henry Parker Manning // Volume II, Mathematical Association of America, 1929. (date of the address: 06.11.2025).