Метод ускоренного вычисления площади круга - Журнал «Наука в мегаполисе Science in the Megapolis»

Аннотация. Данная работа посвящена развитию метода Архимеда, заключающегося в представлении круга, как фигуры, занимающей по площади промежуточное положение между двумя правильными многоугольниками, один из которых является вписанным в окружность с радиусом равным радиусу круга, а другой - описанным вокруг этой окружности. Этот метод был обозначен Архимедом в его трудах по вычислению площади круга, но не был им реализован в практических расчётах. Реализация и усовершенствование этого метода проведены автором статьи.

Ключевые слова: площадь круга, правильный многоугольник, Архимед, Лудольф ван Цейлен, ускоренное вычисление площади круга, число π

Поскольку эта статья, хотя и посвящена новому методу ускоренного вычисления площади круга, но по сути является продолжением многотысячелетних усилий математиков по решению этой задачи, мы считаем необходимым познакомить читателя с историей попыток учёных разных эпох вычислить площадь круга.

Самые древние артефакты, свидетельствующие о попытках решения этой задачи относятся ко 2-му тысячелетию до н.э. В древних египетских математических папирусах для вычисления площади круга использовалась формула: 8/9*8/9*d*d, где d – диаметр круга [3]. По мнению автора статьи, египтяне пришли к этой формуле эмпирически. Если познакомиться с практикой вычислений в Древнем Египте, то становится понятным, как египтяне получили эту формулу. Они могли последовательно сравнивать площадь круга, имеющего диаметр d, с набором квадратов, стороны которых были меньше диаметра круга соответственно на 1/10* d, на 1/9*d, на 1/8*d. Для таких сравнений могли быть использованы фигуры, изготовленные, например, из пластин золота, имеющих равную толщину. Для чего необходимо было иметь всего лишь линейку, циркуль, весы и чистое золото, плюс – умение его обрабатывать. Всё это было у древних египтян.

Наилучшее соответствие по массе, а, соответственно, и по площади, оказалось у круга диаметром d и квадрата со стороной 8/9*d (см. рисунок 1).

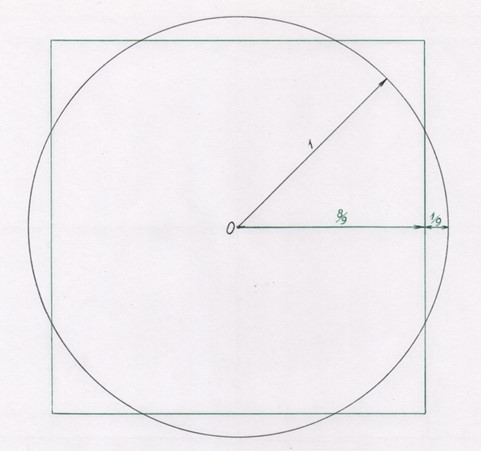
Рис. 1. Египетская квадратура круга

Важно отметить, что египетская квадратура круга имела достаточно высокую точность. Египетская оценка числа π, выраженная как: 4*8/9*8/9 отличалась от истинного значения на величину менее 1%.

Следующим шагом в вычислении числа π была уже теоретическая работа Архимеда по вычислению площади круга. Он установил, что площадь круга равна половине произведения радиуса на периметр круга. Для вычисления периметра Архимед использовал в качестве нижней оценки - периметр вписанного в окружность правильного многоугольника, а в качестве верхней оценки - периметр описанного вокруг окружности правильного многоугольника. Он получил оценку для числа π от 223/71 до 22/7, что немного точнее, чем оценка египтян [1],[2]. Величины периметров вписанного и описанного многоугольников Архимед получал путём умножения рассчитанных длин сторон на число углов в многоугольниках (см. рисунки 2, 3).

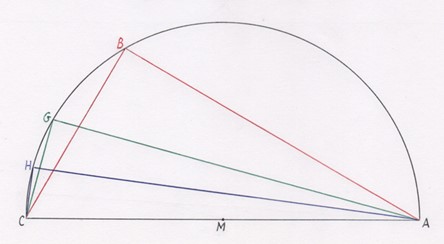
Рис. 2. Иллюстрация Архимеда к методу вычисления стороны вписанного многоугольника [1], [2]

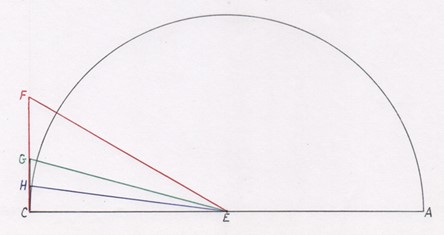
Рис. 3. Иллюстрация Архимеда к методу вычисления стороны описанного многоугольника [1], [2]

Расчёты Архимеда затрудняла сложная система арифметических вычислений. После появления в Европе арабских цифр арифметические вычисления стали проще и голландский математик Лудольф ван Цейлен, основываясь на методе Архимеда, сумел значительно увеличить точность числа π [4], из-за чего число π в XVII веке стали называть числом Лудольфа, хотя справедливее было бы называть число π числом Архимеда, как автора метода его вычисления. В настоящее время, благодаря английскому математику Уильяму Джонсу, вопрос с названием числа π не вызывает споров, хотя косвенно подтверждает приоритет в его вычислении древнегреческого математика Архимеда, так как буква «π» взята из греческого алфавита и является начальной буквой греческого слова «περίμετρον».

Согласимся, что это справедливо, ведь никому же не придёт в голову называть музыкальное произведение не по имени композитора, написавшего его, а по имени наилучшего на сей день его исполнителя.

В наши дни благодаря ЭВМ уже никого не удивишь даже миллиардами знаков в записи числа π. Удивительно другое – что до сих пор никто не заметил гениальной подсказки Архимеда о том, как можно вычислить площадь круга, отталкиваясь не от величины периметров вписанных и описанных многоугольников, а исходя из вычисления непосредственно их площадей. Эта подсказка содержится в чертеже, опубликованном на основе трудов Архимеда (см. рисунок 4).

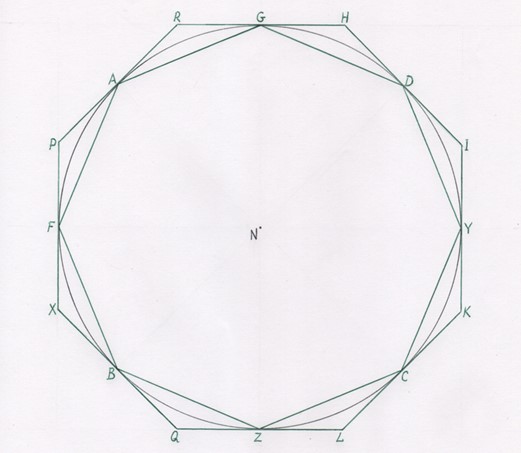
Рис. 4. Иллюстрация Архимеда к методу вычисления непосредственно площади круга [1], [2]

На чертеже просматривается окружность с вписанным и описанным восьмиугольниками. Важно отметить, что первый метод Архимеда при вычислении площади круга предполагает вычисление периметра окружности с последующим умножением на половину радиуса. Второй же метод, требующий вычисления непосредственно площадей вписанных и описанных n-угольников, чтобы затем вычислить промежуточную величину, равную площади круга, Архимед, судя по известным его работам, не использовал, хотя оригинальный чертёж для случая вписанных и описанных восьмиугольников в его книге присутствует. То, что Архимед подразумевал второй способ для вычисления площади круга не через вычисление периметров многоугольников, а именно через вычисление их площадей, косвенно подтверждается тем, что расчёты периметров Архимед проводил для многоугольников, числа углов которых составляют следующий ряд: 6, 12, 24, 48, 96 (этот же ряд использовал в своих вычислениях и Лудольф ван Цейлен). А иллюстрация для расчёта площади круга через площади вписанных и описанных многоугольников приведена для восьмиугольников, то есть для многоугольников из ряда: 4, 8, 16, 32, 64, 128 ... Именно многоугольники из этого ряда мы и будем рассматривать в наших вычислениях.

Гениальность чертежа Архимеда (см. рисунок 4) заключается в том, что вершины вписанных n-угольников совпадают с серединами сторон описанных n-угольников.

Такой чертёж позволяет легко сравнивать приращение площади вписанного n-угольника с урезанием площади описанного n-угольника при увеличении числа углов многоугольников в 2 раза до величины 2n (см. рисунки 5,6).

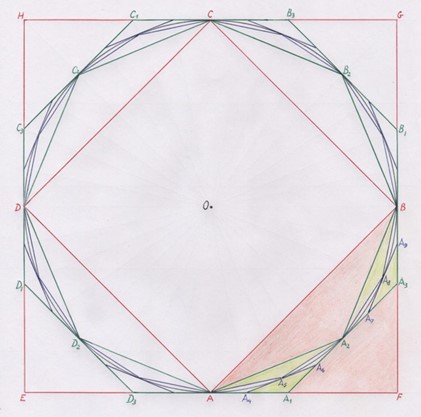
Рис. 5. Приращение и убыль площадей вписанных и описанных 4-угольников и 8-угольников для наглядности выделены цветами (соответственно: красным и жёлтым)

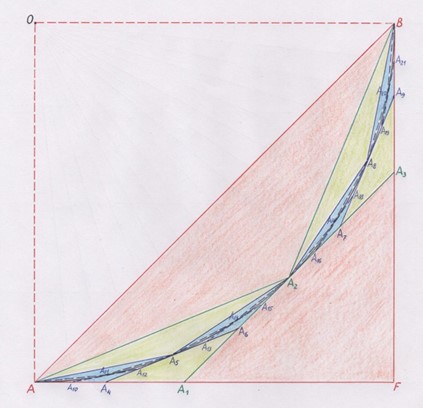
Рис. 6. Приращение и убыль площадей вписанного и описанного 16-угольников выделены синим цветом

Легко доказать, что при n – стремящемся к бесконечности, вписанный n-угольник получает приращение по площади в 2 раза больше, чем составляет убыль площади описанного n-угольника. Использование этого замечательного свойства позволяет быстро получать с высокой точностью значение числа π. Уже на 12-ом шаге вычислений можно получить значение числа π с точностью до 14 знаков после запятой. Автором статьи сведены в таблицу расчётные значения площадей вписанных и описанных многоугольников. При этом полагается, что радиус окружности, на основе которой выполнены построения этих многоугольников, равен единице. Также единице равен квадрат радиуса этой окружности (см. рисунок 7).

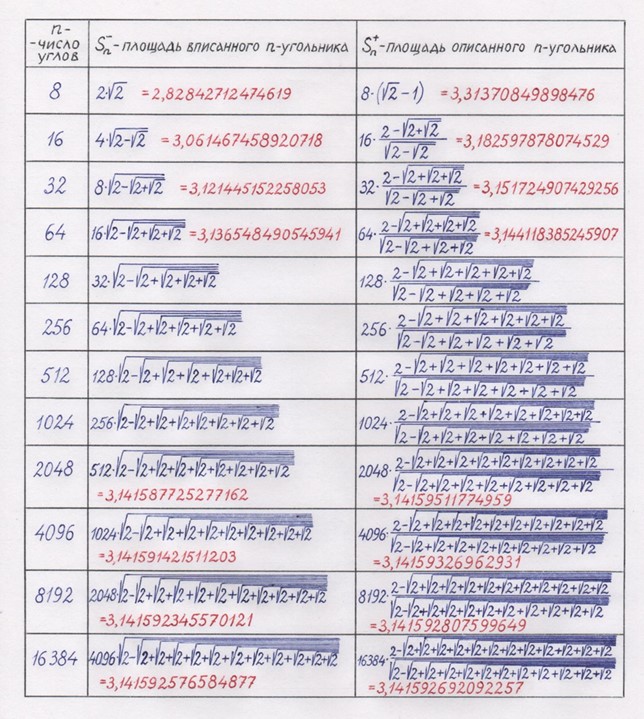
Рис. 7. Таблица площадей вписанных и описанных n-угольников

В следующей таблице приведены значения для оценки площади круга, исходя из рассчитанных площадей вписанных и описанных многоугольников (см. рисунок 8).

Рис. 8. Таблица приблизительных вычислений площади круга на основе вычисленных площадей вписанных и описанных n-угольников

На 12-ом шаге вычислений, когда количество углов правильных многоугольников достигает 16 384, мы получаем значение числа π с точностью до 14-го знака после запятой (см. рисунок 8).

Таким образом, можно считать доказанным эффективность метода ускоренного вычисления площади круга.

Сколько же знаков числа π надо знать, чтобы использовать его в любых научных и технических расчётах?

Начнём с того, что в обычном калькуляторе, которым мы пользуемся для расчётов, можно ввести число π с максимум 15-ю знаками после запятой.

Когда множество ЭВМ тратят своё драгоценное время для расчётов следующих триллионов знаков после запятой в числе π, мне вспоминаются великие египтяне, построившие тысячи лет назад пирамиды, аналогов которых нет в современном мире, и то, что эти египтяне прекрасно обходились при сооружении своих великолепных, величественных храмов и при проведении точных астрономических наблюдений значением числа π с погрешностью меньше 1%.

Список литературы:

The method of accelerated calculation of the area of a circle

Kostyuk V.Y.,
student of 3 course of the Moscow City University, Moscow

Abstract. This work is devoted to the development of Archimedes’ method, that consists in representing a circle as a figure which area value occupies an intermediate position between the areas of two regular polygons, one of which is inscribed in a circle with a radius equal to the radius of the circle, and the other is circumscribed around this circle. This method was indicated by Archimedes in his works on calculating the area of a circle, but was not implemented by him in practical calculations. The implementation and improvement of this method were carried out by the author of the article.
Keywords: area of a circle, regular polygon, Archimedes, Ludolph van Ceulen, accelerated calculation of the area of a circle, the number π.

References:

Archimedes. Two books about the sphere and the cylinder, the circle theory and lemmas. Translation from Greek (Lemmas from Latin) O. Petrushevsky. St. Petersburg: Printing House of the Department of National Education, 1825. 239 p. (date of the address: 24.01.2026).
Archimedis Opera quae extant; novis demonstrationibus commentariisque illustrata. Parisiis [Paris]: apud Claudium Morrellum, via Iacobaea, ad insigne Fontis 1615, 549 p. (date of the address: 25.01.2026).
Arnold Buffum Chace. The Rhind Mathematical Papyrus/Arnold Buffum Chace, Ludlow Bull, Henry Parker Manning // II, Mathematical Association of America, 1929. (date of the address: 26.01.2025).
Ludolph van Ceulen. Ludolphi À Ceulen De Circulo & Adscriptis Liber. Lugd. Batav.: Apud Iodocum à Colster, 1619, 220 p. (date of the address: 27.01.2026).