Выпуск: №7(75) КОД науки - исследования молодых ученых

Раздел: Технические науки и искусственный интеллект

Опубликовано: 20 июня 2025

Код уникальной десятичной классификации: 372.851

Автор: Кузьмина Зинаида Хачатуровна

студент 5 курса, Московский городской педагогический университет (МГПУ), г. Москва, e-mail: GevorkyanZK392@mgpu.ru

Научный руководитель: Кочагина Мария Николаевна

заместитель начальника департамента по учебной работе, доцент департамента математики и физики Института цифрового образования Московского городского педагогического университета (МГПУ)

кандидат педагогических наук, доцент

Аннотация. В современном образовательном пространстве наблюдается растущий интерес к интегративным методикам обучения, среди которых особое место занимает STEM-подход, объединяющий науку, технологии, инженерию и математику. Использование этого подхода в обучении математики в основной школе открывает новые горизонты для формирования у учащихся глубокого понимания предмета и развития ключевых компетенций XXI века, таких как критическое мышление и креативность. В статье описаны возможности использования STEM-подхода в обучении математике учащихся основной школы, представлен инструмент STEM- оборудования, который можно применить при изучении гомотетии и подобия фигур. В статье приведены виды упражнений, раскрывающих применение STEM-оборудования на примере пантографа. Цель исследования – выявить методические особенности использования STEM-подхода при обучении математике учащихся основной школы и разработать соответствующие методические рекомендации. Упражнения, приведенные в статье, были разработаны и апробированы.

Ключевые слова: обучение математике, STEM-подход в образовании, пантограф, виды упражнений.

Перспективы развития STEM-образования в России связаны с введением новых образовательных стандартов, изменений требований к качеству подготовки специалистов, повышением значимости математического и естественно-научного образования [2]. В современном образовательном пространстве наблюдается возрастающий интерес к интегративным методикам обучения, которые призваны преодолеть разрыв между академическими знаниями и их практическим применением. Среди таких методик особое место занимает STEM-подход, объединяющий в себе науку, технологии, инженерию и математику. В контексте основной школы внедрение этого подхода в преподавание математики открывает новые горизонты для формирования у учащихся глубокого понимания предмета и развития ключевых компетенций XXI века. Основное внимание уделяется развитию критического мышления, креативности и способности решать проблемы, что является важным для будущей профессиональной деятельности учащихся [4]. STEM-подход в обучении математике позволяет продемонстрировать учащимся, как математические знания используются в технологических и инженерных решениях, способствующих развитию общества.
Математика в STEM-подходе играет ключевую роль как инструмент моделирования и анализа [7, c. 7]. В рамках такого подхода для изучения различных разделов математики возможно использование инструментов STEM-оборудования, например клинометра-высотомера, разметчика Фибоначчи, измерительного колеса и ряда других [1].

STEM-подход обеспечивает практико-ориентированное образование, позволяя школьникам применять теоретические знания для решения реальных задач, что существенно повышает интерес к учебе и мотивацию к познанию. Его влияние на обучение способствует развитию критического и творческого мышления, стимулируя учащихся самостоятельно искать решения сложных проблем. Это достигается через проектную деятельность, где учащиеся работают над междисциплинарными задачами, требующими применения математических методов в сочетании с технологическими средствами [3].

В условиях быстро меняющегося мира важно не только дать школьникам знания, но и научить их учиться, адаптироваться, мыслить нестандартно. Использование в обучении заданий, требующих интеграции знаний из разных областей, позволяет перейти от суммы разрозненных дисциплин к целостному взгляду на мир, основанному на деятельности учащихся [3]. Учащиеся видят непосредственную связь между тем, что они изучают в классе, и тем, как эти знания могут быть использованы для решения некоторых проблем. Это особенно важно в контексте математического образования, где абстрактность материала часто становится препятствием для понимания и интереса школьников.

Использование STEM-оборудования в современной методической литературе [1, с. 9] рассматривается как одно из направлений реализации STEM-подхода в обучении математике. Среди способов использования STEM-оборудования для обучения математике выделяются следующие [1, с. 11]: знакомство с различными инструментами и целью их использования при изучении соответствующего предметного содержания; выявление математических принципов работы инструментов; выполнение лабораторно-практических работ по математике; решение контекстных заданий при обучении математике; измерение величин разными способами (с использованием STEM-оборудования и без него); самостоятельное конструирование прототипов STEM-инструментов; знакомство с профессиями, в которых используются изучаемые инструменты.

Рассмотрим использование в обучении математике пантографа как одного из STEM-инструментов. Пантограф – это инструмент, который используется для создания увеличенных или уменьшенных копий изображений фигур на плоскости. Пантограф имеет вид раздвижного параллелограмма и состоит из четырех планок (линеек), скрепленных между собой с помощью шарниров так, что линейки способны сдвигаться и раздвигаться, как гармошка (см. рисунок 1).

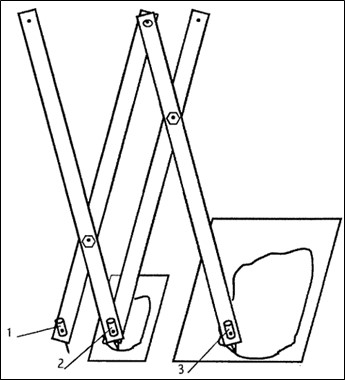
Рис. 1. Устройство пантографа

На концах планок пантографа укреплены игла (полюс), отметчик (шпиль) и карандаш, на рисунке 1 они отмечены цифрами 1, 2 и 3 соответственно. При работе иглу закрепляют в какой-либо точке стола, отметчиком ведут по заданному контуру, а карандаш рисует копию данного контура, но уже в заданном масштабе.

Использование пантографа на уроках геометрии можно начать при изучении подобия фигур и признаков подобия треугольников в 8 классе. Он позволяет наглядно продемонстрировать, как изменяются размеры фигур при соблюдении пропорций, дает возможность учащимся на практике увидеть, как работают признаки подобия треугольников. Пантограф можно использовать в начале урока, чтобы привлечь внимание учащихся и продемонстрировать, как можно создавать подобные фигуры. Это может быть сделано через практическое задание, где учащиеся будут работать с пантографом, создавая копии треугольников. Так же в конце урока можно провести обсуждение результатов работы с пантографом, где учащиеся смогут поделиться своими наблюдениями и выводами о подобии треугольников, что поможет закрепить изученный материал.

Задание 1
Рассмотрите на рисунке 2 устройство пантографа и принцип его работы: 1 – основание; 2 – планка (4 шт.); 3 – «следящий» стержень; 4 – «рисующий» элемент; 5 – винт; 6 – втулка; 7 – шайбы.

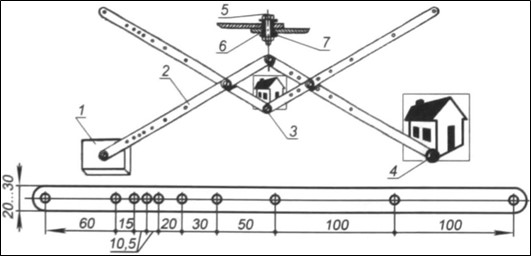
Рис. 2. Устройство пантографа и принцип его работы

Изучите устройство пантографа и принцип его работы, определите:

1. как изменяется масштаб изображения при движении «рисующего» элемента;
2. какие углы между планками сохраняются при работе пантографа.
3. изобразите математическую модель пантографа (раскрыть математические основы работы пантографа).

Учащиеся должны понять механизм работы пантографа и связь с понятием подобия фигур. Задания с пантографом углубляют знания основных свойств треугольника, параллелограмма, подобия и пропорций, связывая их с практическим применением. Средством обучения при выполнении задания является готовый пантограф, взаимодействуя с которым, учащиеся должны понять принцип работы пантографа, а потом соотнести его со схемой.

Следующим этапом применения пантографа в обучении математике в 8-9 классах может стать задание школьникам по самостоятельному конструированию пантографа.

Задание 2
Самостоятельно сконструируйте и соберите пантограф, используя следующую инструкцию:

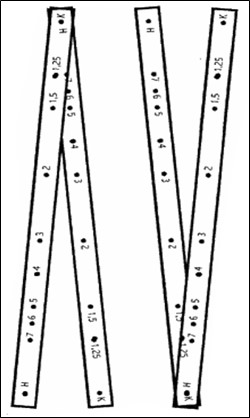
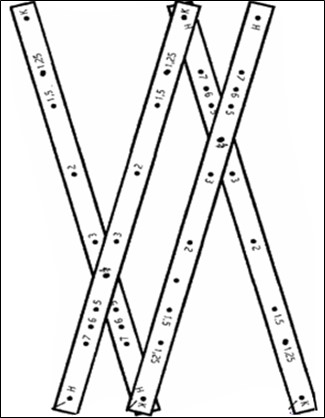
1. Изготовьте четыре линейки из дерева, фанеры или плотного картона (можно воспользоваться готовыми линейками). Две линейки должны быть длиной 630 мм, шириной 15 мм и толщиной 4 мм. Остальные две линейки также имеют длину 630 мм, но ширина и толщина могут быть одинаковыми или отличаться, в зависимости от ваших материалов.

 

Рис. 3. Схема изготовления пантографа

2. На всех линейках разметьте рабочую часть. От концов линейки отложите по 15 мм, чтобы получить рабочую часть длиной 600 мм. Обозначьте начало рабочей части буквой Н, а конец – буквой К (см. рисунок 3).
3. На рабочей части каждой линейки нанесите центры отверстий для настройки пантографа. Для этого разделите длину рабочей части на необходимые коэффициенты увеличения (1,25; 1,5; 2; 3; 4; 5; 6 и 7) и отложите полученные размеры от точки Н. Запишите соответствующие коэффициенты увеличения рядом с отметками.
4. Сделайте отверстия в линейках (можно просверлить) в местах разметки для болтиков (с резьбой М3 или М4). Крайние отверстия в точках Н и К должны быть диаметром 5,6 мм для установки гильз в местах креплений.
5. Соедините линейки попарно с помощью гильз, совмещая конец одной линейки с началом другой.
6. Установите брадсы (болтики) в отверстия с нужным коэффициентом увеличения, выбирая подходящий для работы. Пантограф готов к использованию и может увеличивать оригинал изображения в заданных пропорциях.

В ходе выполнения задания нужно будет выявить закономерности в конструкции и разобраться с математическими зависимостями, лежащими в основе конструкции данного инструмента.

После изготовления совместно с учащимися формулируется алгоритм работы с пантографом:

1. Установите полюс (иглу) пантографа на столе в удобной точке.
2. Разместите рисунок, с которого хотите снять копию, под шпилем пантографа.
3. Поместите чистый лист бумаги под карандашом пантографа.
4. Приготовьтесь к копированию. Если необходимо увеличить рисунок, переходите к следующему шагу. Для уменьшенного изображения поменяйте местами шпиль и карандаш.
5. Ведите шпиль по линиям оригинала, следя за его движением. Карандаш автоматически будет вычерчивать увеличенный рисунок на бумаге.
6. Если рисует рука, которая ведет шпиль, прикрепите груз (гайку или свинцовую пластинку) к линейке рядом с карандашом, чтобы обеспечить прижим к бумаге.
7. В качестве альтернативы можно вести карандаш, следя за движением отметчика. В этом случае груз не нужен, так как карандаш будет вести рука.
8. Завершите копирование, когда все линии оригинала будут перенесены на чистый лист.
9. Проверьте получившийся рисунок на точность и соответствие оригиналу.
10. Далее следуя алгоритму, учащиеся приступают к практическому использованию пантографа при выполнении построений.

Задание 3
С помощью пантографа создайте копию рисунка на листе бумаги. Определите:

1. какие детали оригинала были точно воспроизведены;
2. как изменился размер изображения в зависимости от настроек пантографа.

Учащиеся должны проанализировать свою копию и определить, какие элементы рисунка (например, линии, углы, формы) были воспроизведены точно, а какие – неточно. Это поможет им понять, как работает пантограф и какие факторы влияют на точность копирования. Также они должны заметить, что при изменении настроек пантографа (например, длины рычагов) изменяется масштаб изображения. Учащиеся могут записать, во сколько раз изменился размер копии по сравнению с оригиналом, и сделать выводы о том, как настройки влияют на результат.

Для учащихся, изучающих геометрию углубленно, можно рекомендовать провести практическую работу при изучении гомотетии, выполняя задания с использованием пантографа для построения и анализа треугольников. Учащиеся должны исследовать свойства подобия треугольников, создавая их копии с различными коэффициентами гомотетии, а также доказать, что гомотетия сохраняет прямые и окружности. В результате работы учащиеся представят решения задач и запишут определение гомотетии, объясняя, почему полученные фигуры всегда будут подобны.

На примере пантографа можно познакомить учащихся с шарнирными механизмами, которые они могут сконструировать сами, и рассмотреть математические принципы их работы.

Использование пантографа поможет учащимся увидеть законы математики в природе, технике и окружающем мире и познакомит с инструментом, полезным в профессии архитектора, скульптора, дизайнера, художника, фотографа, ювелира, визажиста и многих других.

Описанный в статье подход стимулирует интерес к изучению математики, побуждает к самостоятельному исследованию и развивает навыки критического мышления. Решение практических задач, требующих применения математических методов в сочетании с технологическими инструментами, позволяет сформировать у школьников понимание междисциплинарных связей и подготовить их к решению комплексных проблем современности.

Список литературы:

1. Кочагина М.Н. Использование STEM-оборудования при обучении математике / М.Н. Кочагина, А.И. Белушкина, А.Д. Звегинцева и др. // Continuum. Математика. Информатика. Образование, 2023. №1(29). С. 8-22.
2. Люблинская И.Е. STEM в школе и новые стандарты среднего естественно-научного образования в США // Проблемы преподавания естествознания в России и за рубежом / Под редакцией Е.Б. Петровой. М.: ЛЕНАНД, 2014. С. 6-23.
3. Обухов А.С., Ловягин С.А. Задания для практики STEM-образования: от суммы частных задач и учебных дисциплин к целостному деятельностному междисциплинарному подходу // Исследователь/Researcher, 2020. №2. С. 63-82.
4. Пинская М.А. Навыки XXI века: как формировать и оценивать на уроке? / М.А. Пинская, А.М. Михайлова, О.А. Рыдзе и др. // Образовательная политика, 2019. №3(79). С. 50-62.
5. Nistor A. Science, Technology, Engineering and Mathematics Education Practices in Europe. Scientix Observatory report. European Schoolnet / A. Nistor, A. Gras-Velazquez, N. Billon, G. Mihai. Brussels, 2018. 80 p.

Pantograph as a stem-tool in teaching mathematics in secondary school

Kuzmina Z.Kh.,
student of 5 course of the Moscow City University, Moscow

Research supervisor:
Kochagina Maria Nikolaevna,
Deputy Head of the Department for Academic Affairs, Associate Professor of the Department of Mathematics and Physics of the Institute of Digital Education of Moscow City University, Candidate of Pedagogical Sciences, Associate Professor

Abstract: In the modern educational space, there is a growing interest in integrative teaching methods, among which the STEM, combining science, technology, engineering and mathematics, occupies a special place. Using this approach in teaching mathematics in secondary schools opens up new horizons for students to develop a deep understanding of the subject and develop key competencies of the 21st century, such as critical thinking and creativity. The article describes the possibilities of using the STEM in teaching mathematics to primary school students, and presents a STEM-equipment tool that can be used in the study of homothety and similarity of shapes. The article presents the types of exercises that reveal the use of STEM-equipment using the example of a pantograph. The purpose of the study is to identify the methodical features of using the STEM in teaching mathematics to primary school students and to develop appropriate Methodic recommendations in the article have been developed and tested.
Keywords: teaching mathematics, STEAM approach in education, pantograph, types of exercises.

References:

1. Kochagina M.N. Using STEM-equipment in teaching mathematics / M.N. Kochagina, A.I. Belyshkina, A.D. Zvyagintseva et al // Continuum. Mathematics. Computer science. Education. 2023, №1(29).: 8-22.
2. Leblinskaya I.E. STEM of education and new approaches to public scientific education in USA // Problems of youth education in Russia and abroad / Edited by E.B. Petrova. Moscow: LENINGRAD, 2014.: 6-23.
3. Obukhov A.S., Lovyagin S.A. Tasks for STEM education practice: from the sum of particular tasks and academic disciplines to a holistic activity-based interdisciplinary approach // Researcher/Researcher, 2020. №2.: 63-82.
4. Pinskaya M.A. Novices of the XXI century: how to formulate and interpret in the lesson? / M.A. Pinskaya, A.M. Mikhailova, O.A. Redze et al. // Educational Policy, 2019. №3(79).: 50-62.
5. Nistor A. The practice of education in science, technology, engineering and mathematics in Europe. The report of the Scientix Observatory. The European School Network / A. Nistor, A. Grass-Velasquez, N. Billon, G. Mihai. Brussels, 2018. 80 p.